You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
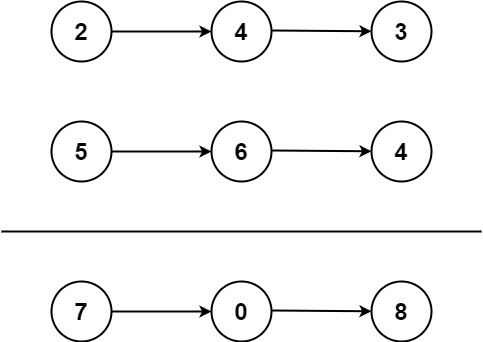
Input: l1 = [2,4,3], l2 = [5,6,4] Output: [7,0,8] Explanation: 342 + 465 = 807.
Example 2:
Input: l1 = [0], l2 = [0] Output: [0]
Example 3:
Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] Output: [8,9,9,9,0,0,0,1]
Constraints:
- The number of nodes in each linked list is in the range
[1, 100]. 0 <= Node.val <= 9- It is guaranteed that the list represents a number that does not have leading zeros.
Problem Description
Imagine you have two numbers, but instead of writing them down in the usual way, you write each digit down separately, in reverse order, and then link all these digits together into a chain where each link is a single digit. These chains are what we call linked lists in computer science, and each digit lives in its own node, a little container with the number and a pointer to the next digit in the list.
Now, let’s say someone gives you two of these chains, both representing non-negative integers, and asks you to add these numbers together just like you would on a piece of paper. But here’s the twist: the result should be presented in the same reversed chain format.
The problem resembles simple addition, starting from the least significant digit (which is at the head of the chain because of the reverse order) and moving up to the most significant one, carrying over any overflow.
And there’s one more thing – if our numbers were zeroes, they wouldn’t have any leading digits, except for a single zero node to represent the number itself.
The challenge here is to simulate this familiar arithmetic operation using the rules and structures of linked lists.
Intuition
Adding two numbers is something we learn early in school, and the process is almost second nature – start with the rightmost digits, add them, carry over if needed, and move left. Doing this with linked lists means mimicking this step-by-step addition. However, linked lists don’t allow us to access an element directly by position; we traverse from the start node to the end node.
We start the simulation by simultaneously walking down both linked lists – these are our two numbers in reverse order. At each step, we sum the current digit of each number along with any carry left over from the previous step.
We keep track of the carry-over because, during addition, if we add two digits and the sum is 10 or higher, we need to carry over the ‘1’ to the next set of digits. In coding terms, think of ‘carry’ as a temporary storage space where we keep that extra digit.
To hold our resulting number, we create a new linked list (we’ll call it the ‘sum list’). For each pair of digits we add, we’ll create a new node in the ‘sum list’ that contains the result of the addition modulo 10 (which is the remainder after division by 10 – basically, the digit without the carry part). The carry (if any) is computed as the floor division of the sum by 10.
We continue traversing both input lists, adding corresponding digits and carry as we go. If one list is longer, we simply carry on with the digits that remain. After we’ve exhausted both lists, if there’s still a carry, it means we need one more node with the value of the carry.
When we’re done adding, we simply return the head of our ‘sum list’, and voilà, that’s our total, neatly reversed just as we started.
Solution Approach
As outlined in the reference solution approach, we simulate the addition process using a simple iterative method. In computational terms, this is relatively straightforward.
Firstly, we need a placeholder for the sum of the two numbers, which in this case will be a new linked list. We create a dummy node that acts as the head of our sum list. This dummy node is very handy because it allows us to easily return the summed list at the end, avoiding the complexities of handling where the list begins in the case of an overflow on the most significant digit.
We initialize two variables:
- The
carryvariable (starting at0), to keep track our carryover in each iteration. - The
currvariable, which points to the current node in the sum list; initially, this is set to thedummynode.
We enter a loop that traverses both input linked lists. The loop continues as long as at least one of the following conditions holds true: there is at least one more node in either l1 or l2, or there is a non-zero value in carry. Within the loop:
- We sum the current digit from each list (
l1.valandl2.val) with the current carry. If we’ve reached the end of a list, we treat the missing digits as0. - The sum produced can be broken down into two parts: the digit at the current position, and the carryover for the next position. This is computed using
divmod(s, 10)which gives us the quotient representingcarryand the remainder representingval– the current digit to add to our sum list. - We create a new node for
valand find its place at the end of the sum list indicated bycurr.next. - We update
currto point to this newly added node. - We update
l1andl2to point to their respective next nodes – moving to the next digit or setting toNoneif we’ve reached the end of the list.
The loop exits once there are no more digits to add and no carry. Since dummy was only a placeholder, the actual resultant list starts from dummy.next.
Lastly, we return dummy.next, which points to the head of the linked list representing the sum of our two numbers. The way our loop is structured ensures that this process carries out the addition operation correctly for linked lists of unequal lengths as well, without any additional tweaks or condition checks.
Example Walkthrough
To illustrate the solution approach, consider two linked lists representing the numbers 342 and 465. The linked lists would look like this:
l1: 2 -> 4 -> 3 (Representing 342 written in reverse as a linked list)l2: 5 -> 6 -> 4 (Representing 465 written in reverse as a linked list)
According to the solution:
- Initialize a
dummynode to serve as the head of the new linked list that will store our result. - Set a
carryvariable to0andcurrto point todummy. - Iterate over
l1andl2as long as there is a node in either list orcarryis not zero.For the first iteration:l1.valis2, andl2.valis5. The sum is2 + 5 + carry (0) = 7.- The digit for the new node is
7 % 10 = 7, and the new carry is7 // 10 = 0. - Create a new node with a value of
7and link it tocurr.
The resulting list is now 7, the dummy node points to 7, and curr also points to 7.
Continuing to the second digit:
l1.valis4,l2.valis6. The sum is4 + 6 + carry (0) = 10.- The digit for the new node is
10 % 10 = 0, and the new carry is10 // 10 = 1. - Create a new node with a value of
0and link it tocurr.
Now, the resulting list is 7 -> 0, dummy points to 7, and curr points to 0.
For the third digit:
l1.valis3,l2.valis4. The sum is3 + 4 + carry (1) = 8.- The digit for the new node is
8 % 10 = 8, and the new carry is8 // 10 = 0. - Create a new node with a value of
8and link it tocurr.
Our final list becomes 7 -> 0 -> 8, which is the reverse of 807, the sum of 342 and 465.
After the end of the loop, we check to see if carry is non-zero. In this case, it’s zero, so we do not add another node.
Lastly, since the dummy was just a placeholder, we return dummy.next, which gives us 7 -> 0 -> 8, the final linked list representing our summed number in reverse order.
Solution Implementation
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
// Create a dummy node to simplify the result list construction
ListNode* dummy = new ListNode(0);
ListNode* current = dummy; // Pointer to track the current position in the result list
int carry = 0; // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while (l1 != nullptr || l2 != nullptr) {
// Extract the current values from l1 and l2, defaulting to 0 if a list is exhausted
int x = (l1 != nullptr) ? l1->val : 0;
int y = (l2 != nullptr) ? l2->val : 0;
// Calculate the sum of the two digits plus the carry
int sum = carry + x + y;
// Update carry for the next iteration (sum divided by 10)
carry = sum / 10;
// Create a new node for the result list with the current sum's ones digit
current->next = new ListNode(sum % 10);
current = current->next; // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if (l1 != nullptr) l1 = l1->next;
if (l2 != nullptr) l2 = l2->next;
}
// If there is any remaining carry, create a new node for it
if (carry > 0) {
current->next = new ListNode(carry);
}
// Return the next node of dummy as it is a placeholder
return dummy->next;
}
};class Solution {
public ListNode addTwoNumbers(ListNode L1, ListNode L2) {
// Create a new head node for the result linked list
ListNode head = new ListNode();
ListNode prev = head; // Pointer to track the previous node
int carry = 0; // Initialize carry as 0 to start the addition
// Traverse both lists L1 and L2 until both are null and there's no carry left
while(L1 != null || L2 != null || carry != 0){
int op1 = 0; // Initialize first operand as 0
int op2 = 0; // Initialize second operand as 0
// If L1 is not null, get the value of the current node and move to the next node
if (L1 != null) {
op1 = L1.val;
L1 = L1.next;
}
// If L2 is not null, get the value of the current node and move to the next node
if (L2 != null) {
op2 = L2.val;
L2 = L2.next;
}
// Calculate the sum of the current digits plus the carry
int sum = op1 + op2 + carry;
// Update the carry for the next iteration (sum divided by 10)
carry = sum / 10;
// Create a new node for the current digit (sum minus carry * 10)
ListNode result = new ListNode(sum - carry * 10);
// Link the result node to the previous node
prev.next = result;
// Move the previous pointer to the current result node
prev = result;
}
// Return the head of the result list (skip the dummy head node)
return head.next;
}
}class Solution(object):
def addTwoNumbers(self, l1, l2):
# Create a dummy node to simplify result list construction
dummy = ListNode(0)
current = dummy # Pointer to track the current position in the result list
carry = 0 # Initialize carry as 0 for the addition
# Iterate through both lists until both are exhausted
while l1 is not None or l2 is not None:
# Get the current value from l1 and l2, defaulting to 0 if a list is exhausted
x = l1.val if l1 is not None else 0
y = l2.val if l2 is not None else 0
# Calculate the sum of the two digits plus the carry
sum = carry + x + y
# Update carry for the next iteration (integer division by 10)
carry = sum // 10
# Create a new node for the result list with the current sum's ones digit
current.next = ListNode(sum % 10)
current = current.next # Move to the next node in the result list
# Move to the next nodes in l1 and l2 if they exist
if l1 is not None: l1 = l1.next
if l2 is not None: l2 = l2.next
# If there is any remaining carry, create a new node for it
if carry > 0:
current.next = ListNode(carry)
# Return the next node of dummy as it is a placeholder
return dummy.nextstruct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2) {
struct ListNode dummy;
struct ListNode* current = &dummy;
int carry = 0;
dummy.next = NULL;
while (l1 != NULL || l2 != NULL) {
int x = (l1 != NULL) ? l1->val : 0;
int y = (l2 != NULL) ? l2->val : 0;
int sum = carry + x + y;
carry = sum / 10;
current->next = (struct ListNode*)malloc(sizeof(struct ListNode));
current->next->val = sum % 10;
current->next->next = NULL;
current = current->next;
if (l1 != NULL) l1 = l1->next;
if (l2 != NULL) l2 = l2->next;
}
if (carry > 0) {
current->next = (struct ListNode*)malloc(sizeof(struct ListNode));
current->next->val = carry;
current->next->next = NULL;
}
return dummy.next;
}public class Solution {
public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {
// Create a dummy node to simplify the result list construction
ListNode dummy = new ListNode(0);
ListNode current = dummy; // Pointer to track the current position in the result list
int carry = 0; // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while (l1 != null || l2 != null) {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
int x = (l1 != null) ? l1.val : 0;
int y = (l2 != null) ? l2.val : 0;
// Calculate the sum of the two digits plus the carry
int sum = carry + x + y;
// Update carry for the next iteration (sum divided by 10)
carry = sum / 10;
// Create a new node for the result list with the current sum's ones digit
current.next = new ListNode(sum % 10);
current = current.next; // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if (l1 != null) l1 = l1.next;
if (l2 != null) l2 = l2.next;
}
// If there is any remaining carry, create a new node for it
if (carry > 0) {
current.next = new ListNode(carry);
}
// Return the next node of dummy as it is a placeholder
return dummy.next;
}
}var addTwoNumbers = function (l1, l2) {
// Initialise a new ListNode to be returned
var newListNode = new ListNode(0);
var headOfNewListNode = newListNode;
// Initialise variables to be utilised on each run
var sum = 0;
var carry = 0;
// While there are elements (or a carried number) to add
while (l1 !== null || l2 !== null || sum > 0) {
// If there's an element in l1 to be added, add it to the sum and move to the next l1 node
if (l1 !== null) {
sum = sum + l1.val;
l1 = l1.next;
}
// If there's an element in l2 to be added, add it to the sum and move to the next l2 node
if (l2 !== null) {
sum = sum + l2.val;
l2 = l2.next;
}
// Check if the sum for these nodes exceeds 10
if (sum >= 10) {
carry = 1;
sum = sum - 10;
}
// Add the sum to the new ListNode, and then move it to the next entry
headOfNewListNode.next = new ListNode(sum);
headOfNewListNode = headOfNewListNode.next;
// Set the sum for the next addition to equal the carry-over (if there was one)
sum = carry;
carry = 0;
}
// Return the constructed ListNode (ignoring the first dummy entry)
return newListNode.next;
};function addTwoNumbers(l1: ListNode | null, l2: ListNode | null): ListNode | null {
// Create a dummy node to simplify the result list construction
let dummy = new ListNode(0);
let current = dummy; // Pointer to track the current position in the result list
let carry = 0; // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while (l1 !== null || l2 !== null) {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
let x = (l1 !== null) ? l1.val : 0;
let y = (l2 !== null) ? l2.val : 0;
// Calculate the sum of the two digits plus the carry
let sum = carry + x + y;
// Update carry for the next iteration (sum divided by 10)
carry = Math.floor(sum / 10);
// Create a new node for the result list with the current sum's ones digit
current.next = new ListNode(sum % 10);
current = current.next; // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if (l1 !== null) l1 = l1.next;
if (l2 !== null) l2 = l2.next;
}
// If there is any remaining carry, create a new node for it
if (carry > 0) {
current.next = new ListNode(carry);
}
// Return the next node of dummy as it is a placeholder
return dummy.next;
}class Solution {
function addTwoNumbers($l1, $l2) {
// Create a dummy node to simplify the result list construction
$dummy = new ListNode(0);
$current = $dummy; // Pointer to track the current position in the result list
$carry = 0; // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while ($l1 !== null || $l2 !== null) {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
$x = ($l1 !== null) ? $l1->val : 0;
$y = ($l2 !== null) ? $l2->val : 0;
// Calculate the sum of the two digits plus the carry
$sum = $carry + $x + $y;
// Update carry for the next iteration (sum divided by 10)
$carry = (int)($sum / 10);
// Create a new node for the result list with the current sum's ones digit
$current->next = new ListNode($sum % 10);
$current = $current->next; // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if ($l1 !== null) $l1 = $l1->next;
if ($l2 !== null) $l2 = $l2->next;
}
// If there is any remaining carry, create a new node for it
if ($carry > 0) {
$current->next = new ListNode($carry);
}
// Return the next node of dummy as it is a placeholder
return $dummy->next;
}
}class Solution {
func addTwoNumbers(_ l1: ListNode?, _ l2: ListNode?) -> ListNode? {
// Create a dummy node to simplify the result list construction
let dummy = ListNode(0)
var current = dummy // Pointer to track the current position in the result list
var carry = 0 // Initialize carry as 0 for the addition
var l1 = l1 // Initialize l1 for iteration
var l2 = l2 // Initialize l2 for iteration
// Iterate through both lists until both are exhausted
while l1 != nil || l2 != nil {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
let x = l1?.val ?? 0
let y = l2?.val ?? 0
// Calculate the sum of the two digits plus the carry
let sum = carry + x + y
// Update carry for the next iteration (sum divided by 10)
carry = sum / 10
// Create a new node for the result list with the current sum's ones digit
current.next = ListNode(sum % 10)
current = current.next! // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if l1 != nil { l1 = l1?.next }
if l2 != nil { l2 = l2?.next }
}
// If there is any remaining carry, create a new node for it
if carry > 0 {
current.next = ListNode(carry)
}
// Return the next node of dummy as it is a placeholder
return dummy.next
}
}class Solution {
fun addTwoNumbers(l1: ListNode?, l2: ListNode?): ListNode? {
// Create a dummy node to simplify the result list construction
val dummy = ListNode(0)
var current: ListNode? = dummy // Pointer to track the current position in the result list
var p = l1 // Pointer for the first linked list
var q = l2 // Pointer for the second linked list
var carry = 0 // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while (p != null || q != null) {
// Get the current values from p and q, defaulting to 0 if a list is exhausted
val x = p?.`val` ?: 0
val y = q?.`val` ?: 0
// Calculate the sum of the two digits plus the carry
val sum = carry + x + y
// Update carry for the next iteration (sum divided by 10)
carry = sum / 10
// Create a new node for the result list with the current sum's ones digit
current?.next = ListNode(sum % 10)
current = current?.next // Move to the next node in the result list
// Move to the next nodes in p and q if they exist
if (p != null) p = p.next
if (q != null) q = q.next
}
// If there is any remaining carry, create a new node for it
if (carry > 0) {
current?.next = ListNode(carry)
}
// Return the next node of dummy as it is a placeholder
return dummy.next
}
}class Solution {
ListNode? addTwoNumbers(ListNode? l1, ListNode? l2) {
// Create a dummy node to simplify the result list construction
ListNode dummy = ListNode(0);
ListNode current = dummy; // Pointer to track the current position in the result list
int carry = 0; // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
while (l1 != null || l2 != null) {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
int x = (l1 != null) ? l1!.val : 0;
int y = (l2 != null) ? l2!.val : 0;
// Calculate the sum of the two digits plus the carry
int sum = carry + x + y;
// Update carry for the next iteration (sum divided by 10)
carry = sum ~/ 10;
// Create a new node for the result list with the current sum's ones digit
current.next = ListNode(sum % 10);
current = current.next!; // Move to the next node in the result list
// Move to the next nodes in l1 and l2 if they exist
if (l1 != null) l1 = l1.next;
if (l2 != null) l2 = l2.next;
}
// If there is any remaining carry, create a new node for it
if (carry > 0) {
current.next = ListNode(carry);
}
// Return the next node of dummy as it is a placeholder
return dummy.next;
}
}func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
// Create a dummy node to simplify the result list construction
dummy := &ListNode{}
current := dummy // Pointer to track the current position in the result list
carry := 0 // Initialize carry as 0 for the addition
// Iterate through both lists until both are exhausted
for l1 != nil || l2 != nil {
// Get the current values from l1 and l2, defaulting to 0 if a list is exhausted
x := 0
if l1 != nil {
x = l1.Val
l1 = l1.Next
}
y := 0
if l2 != nil {
y = l2.Val
l2 = l2.Next
}
// Calculate the sum of the two digits plus the carry
sum := carry + x + y
// Update carry for the next iteration (sum divided by 10)
carry = sum / 10
// Create a new node for the result list with the current sum's ones digit
current.Next = &ListNode{Val: sum % 10}
current = current.Next // Move to the next node in the result list
}
// If there is any remaining carry, create a new node for it
if carry > 0 {
current.Next = &ListNode{Val: carry}
}
// Return the next node of dummy as it is a placeholder
return dummy.Next
}Time and Space Complexity
Time Complexity
The time complexity of the given code is O(max(m, n)), where m and n are the lengths of the input linked lists l1 and l2, respectively. This is because we iterate through both lists in parallel, and at each step, we add the corresponding nodes’ values along with any carry from the previous step, which takes constant time O(1). The iteration continues until both lists have been fully traversed and there is no carry left to add.
Space Complexity
The space complexity of the code is O(1), ignoring the space consumption of the output list. The variables carry, curr, and the nodes we iterate through (l1 and l2) only use a constant amount of space. However, if we take into account the space required for the result list, the space complexity would be O(max(m, n)), since in the worst case, the resultant list could be as long as the longer of the two input lists, plus one extra node for an additional carry.

Some really wondrous work on behalf of the owner of this web site, perfectly great written content.